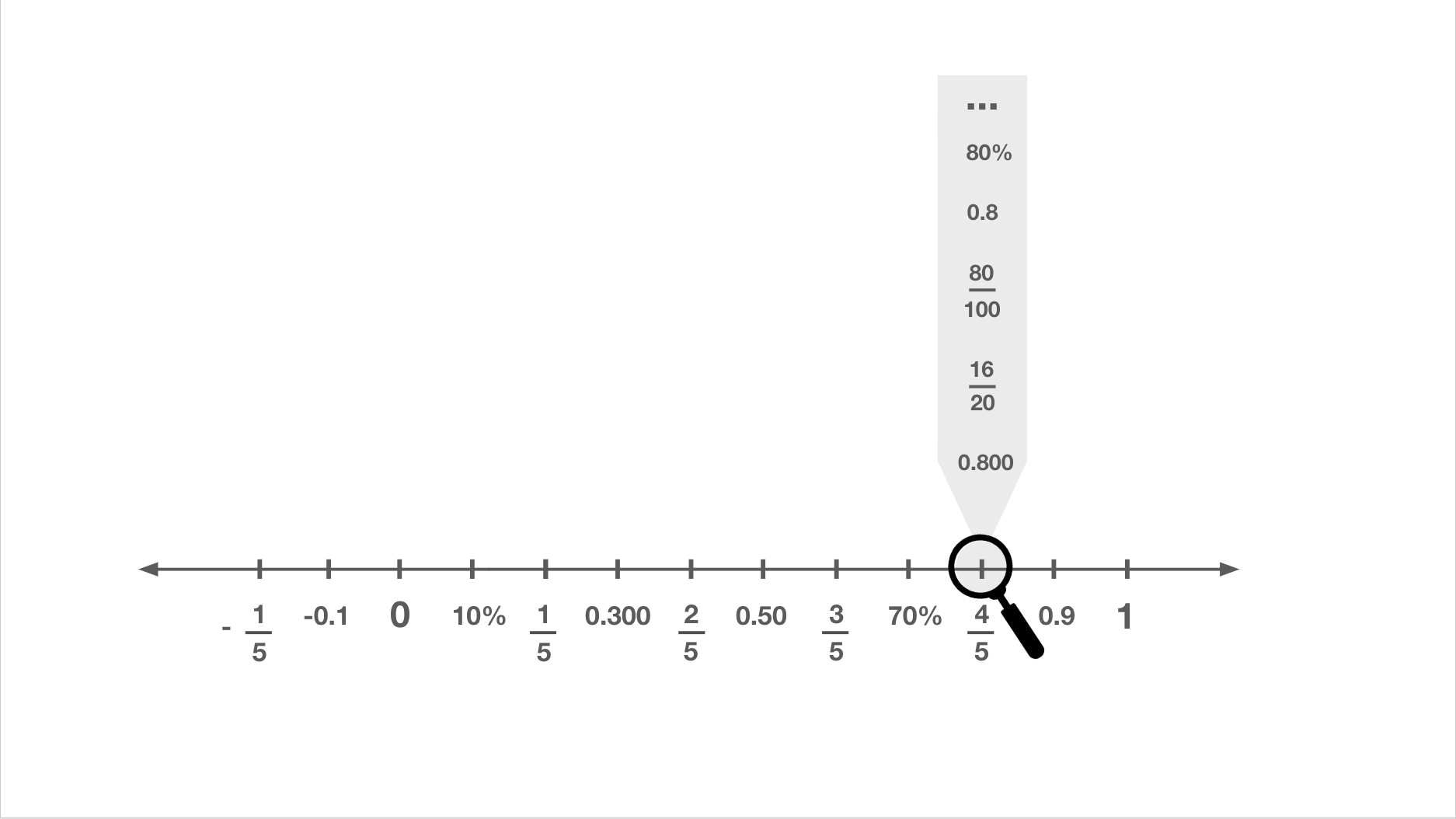
Figure 1. Visual representation of an integrated mental number line adapted from Schiller & Siegler (2023), Cognitive Development.

My research focuses on the integration of knowledge, a vital human capacity that allows for critical thinking, creativity, and collaboration. First, I seek to understand how people integrate knowledge from multiple domains and apply it within specific contexts. Second, I use these insights to develop interventions to facilitate application of knowledge in relevant contexts.

            I investigate integration of knowledge in the domain of mathematics, a foundational knowledge set with consequences for health and monetary-related life outcomes (Murnane et al., 1995; Siegler et al., 2011, 2012; Thompson et al., 2022). Specifically, my research program examines the integration of numerical knowledge (e.g., fractions, decimals, percentages) and its application to specific contexts (e.g. health statistics). A typical measure of numerical knowledge is magnitude comparison, which involves asking participants to select the larger of two numbers. Decades of research have focused on within-notation numerical knowledge (e.g., comparing fractions to fractions or decimals to decimals). I argue that measures of within-notation knowledge fail to capture integration of knowledge. I contend that instead, cross-notation comparison (e.g., comparing fractions to decimals or percentages to fractions) reveals important information about learners’ degree of integration. My research suggests (1) students with better integrated number sense – the ability to fluidly compare magnitudes within and across notations – have better math outcomes (Schiller & Siegler, 2023), and (2) integrated number sense can be improved through instruction (Schiller, 2020; Schiller et al., in press).

Integrated knowledge supports achievement. Just as individuals must come to understand that counting numbers refer to the quantity of the set (Le Corre & Carey, 2007), individuals must come to understand that each number can be represented in infinite ways (Figure 1). Within-notation understanding of each rational number notation has been shown to explain variance in math achievement (Siegler et al., 2011). I contend, however, that it is not simply enough to understand fraction, decimal, or percent magnitudes alone, students must integrate their knowledge to understand the equivalencies between the formats. Based on this reasoning, I theorized that cross-notation understanding should explain variance in math achievement beyond that explained by within-notation understanding. Indeed, I have shown that cross-notation comparison accuracy explains variance in children’s standardized test scores (Schiller & Siegler, 2023) and adults’ self-reported SAT/ACT scores (Schiller et al., in press). These results highlight that integrated number sense, as measured by cross-notation comparison ability, is indeed a critical component of numerical development and provides an equitable foundation for math achievement for all (Moses, 2005)